РЕШЕНИЕ ЗАДАЧИ № для КЛАССА

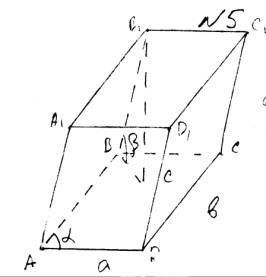Дано: A-C₁ — косой паралепипед, V=1 .
Доказать, что хоть одно расстояние между какими-то вершинами не менее √3 .

Доказательство:
AD = a, DC = b, AA₁ = c.
Угол между AB и BC = A .
Угол между (ABC) и CC₁ = B .
V=S_abcd*h=a*b*c*sin(A)*sin(B)=1 .
a*b*c≥1 , следовательно, a² + b² + c² ≥ 3 .
Пусть AC>BD .
Тогда AC² = a² + b² + 2ab*cos(A)
Тогда AC₁² = a² + b² + c² + 2*AC*c*cos(B) + 2*ab*cos(A)
Но т.к. a² + b² + c² ≥ 3, следовательно и AC₁² ≥3 , следовательно, AC₁ ≥ √3 , ч.т.д.

(автор решения – Гуренков Михаил, г. Москва, центр образования «Царицыно» № 548)


РЕШЕНИЯ ДРУГИХ ЗАДАЧ:



Федотов Валерий Павлович , 2001-2006гг., контент и дизайн сайта по технологии "барокко".